Lo chiameremo paraboloide……

Dissertazione quasi seria sui “sili a sezione parabolica” dell’area ex Montedison di S.Maria degli Angeli

Parte prima. Il nome: breve viaggio nella geometria delle coniche

vai alla pagina Riccardo Morandi, Pierluigi Nervi, riepilogativa del sito ex Montedison

schizzo di Alberto Capitanucci

di Alberto Capitanucci – 08/07/18

Nella lingua italiana, la presenza del suffisso “-oide” fa intendere che si è davanti ad un’entità cui si attribuisce una “somiglianza di forma, di aspetto, di natura o comunque relazione, analogia, affinità con la cosa indicata dalla parola cui <detto suffisso> viene aggiunto“. (1)
Nell’accezione comune, non sempre in linea con quella scientifica,“-oide” ci mette sull’avviso rispetto all’automatica identificazione dell’oggetto della nostra attenzione con parti della realtà con cui si è stabilita naturale confidenza: il termine “umanoide”, nella forma aggettivale corrente non equivale ad un complimento e, quando elevato a sostantivo,riporta ad immagini di saghe interstellari o ad epiche della preistoria profonda. In generale, il suffisso “–oide”, da semplice, grammaticale, “espansore” della realtà compiutamente definita, è divenuto marchio di una sgradevole indeterminatezza.
Nessuno di noi può affermare che siederebbe volentieri vicino ad un “umanoide” o che può provare piacere ad essere definito “intellettualoide”. Tuttavia, entrando nel campo della geometria, il suffisso “–oide”perde di “pericolosità” e, anzi, fa acquistare al morfema cui si aggancia un senso di positiva e compiaciuta partecipazione alla complessità.
Il quadrato e il rettangolo sono figure “immediate”, così pure il trapezio, definire il rombo ci impegna appena di più ma, siamo in grado di dire cosa sia il “romboide”? No, il “romboide” no. A dispetto di Euclide che, nella sua XXII definizione (2) accorpa ed esplicita tutte le figure quadrilatere,  senza eccezioni, il richiamo al “romboide” ci proietta in una sorta di universo superiore dal quale ci sentiamo attratti pur consci di non essere preparati ad entrarvi.

schizzo di Alberto Capitanucci

Lasciamo Euclide (IV sec. a.C.) e incontriamo Apollonio di Perga (III sec. a.C.) al quale si deve la moderna definizione di “cono” e, conseguentemente, la formulazione delle tre “curve coniche”, ovvero ellisse, iperbole e parabola, originate ciascuna da piani diversamente secanti la (le) falda (e) del cono. Pur rimanendo ancora nel campo della geometria elementare, la familiarità che sentiamo – in particolare per “parabola” – deriva più dalla trasposizione dei termini nel campo della retorica che non dalla consuetudine alla frequentazione dei “luoghi geometrici”.
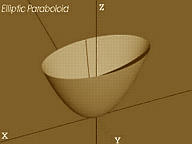
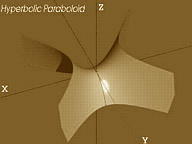
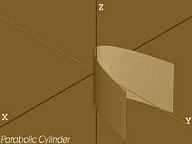
Dalle tre “coniche”, ripetiamo, curve nel piano, il passaggio nel mondo delle superfici, nello “spazio” significa parlare di “quadriche”, superfici algebriche di secondo ordine, nel cui insieme vanno annoverati cono, cilindro e sfera ma, anche superfici per così dire, meno familiari per le quali torna utilissimo il suffisso con cui si è dato inizio a questa conversazione: ellissoide, iperboloidea singola e doppia falda, paraboloide ellittico e paraboloide iperbolico.
A questo punto, evitando di addentrarci in noiose definizioni analitiche, e facendo riferimento alle immagini che seguono, chiariamo che di entità “paraboloidi” ne esistono due: il paraboloide iperbolico e il paraboloide ellittico.

Paraboloide iperbolico

Paraboloide ellittico

Anche un osservatore poco attento non avrà difficoltà a riconoscere che con i cosiddetti “paraboloidi Nervi e Morandi” le superfici citate ben poco hanno a che fare.

La cosiddetta “Struttura Morandi”

La cosiddetta “Struttura Nervi”

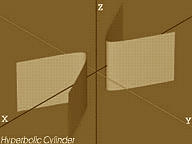
Difatti, si tratta non di “paraboloidi” ma, di “cilindri” ovvero superfici luogo geometrico delle rette parallele a una retta data, passanti per i punti di una data curva (direttrice del cilindro, aperta o chiusa che sia).

Cilindro ellittico

Cilindro iperbolico

Cilindro parabolico

Se la direttrice è una conica (cilindro “quadrico”) e, in specifico una parabola, la superficie che viene a crearsi con lo “scorrere” della retta generatrice sulla curva direttrice è il cilindro parabolico.
Il disegno che segue si riferisce a quella che viene considerata la prima grande struttura a volta parabolica italiana, realizzata nei primi anni venti del secolo scorso a Casale Monferrato (progetto ingegner Radici, Bergamo), circa trenta anni prima delle strutture di Santa Maria degli Angeli.
Che l’ingegner Radici padroneggiasse geometria e statica è fuor d’ogni dubbio, eppure il titolo di questa bellissima tavola tecnica è, nella sua pragmatica semplicità, “SILOS per KINKLER”.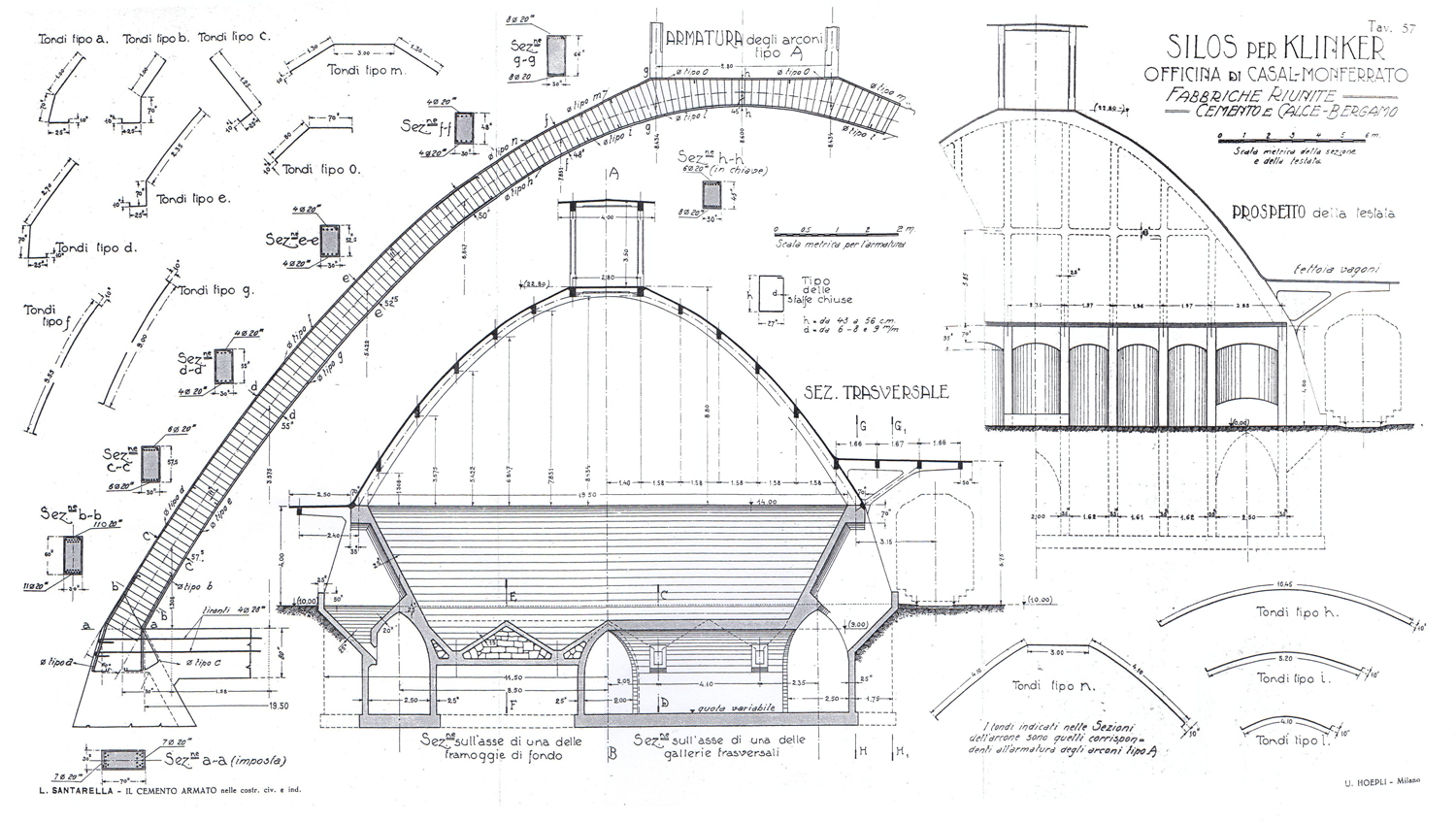
Oggi, un’intera sezione del sito istituzionale del Comune di Casale Monferrato è dedicata al “Paraboloide”, lettera iniziale maiuscola.
Evidentemente a Casale,  come ad Assisi o a Porto Recanati, il nome derivante dalla destinazione d’uso non conferiva a questi “oggetti” l’enfasi desiderata, necessità peraltro del tutto estranea agli anni della costruzione degli stessi. Ancor meno ispirante deve essere parso il ricondursi alla “specie” geometrica dei cilindri parabolici, poiché del “cilindro” pochi sono i tratti appartenenti al senso comune del termine.
Fortunatamente, in soccorso dei moderni tassonomisti, il suffisso“-oide”si è agganciato alla radice, ottenendo, con buona pace di Apollonio di Perga, un nome dal suono “giusto” ancorché scientificamente inesatto e disancorato dalle origini: paraboloide (….lettera iniziale minuscola).

(1) http://www.treccani.it/vocabolario/oide/
òide [dal gr. -οειδής, dove -o- è la vocale tematica della parola precedente e -ειδής l’elemento compositivo che significa«simile a», affine a εἶδος «aspetto»; lat. -oīdes]. – 1. Suffisso di numerose parole composte derivate dal greco (come adenoide, antropoide, romboide, da ἀδηνοειδής, propr. «che ha forma di ghiandola», ἀνϑρωποειδής «simile a uomo», ῥομβοειδής «che ha forma di rombo o losanga»), o più spesso formate modernamente sul modello greco, nelle quali indica in genere somiglianza di forma, di aspetto, di natura o comunque relazione, analogia, affinità con la cosa indicata dalla parola cui viene aggiunto.

2) Libro I degli Elementi, XXII def. – Delle figure quadrilatere, è quadrato quella che è insieme equilatera ed ha gli angoli retti, rettangolo quella che ha gli angoli retti ma non è equilatera, rombo quella che è equilatera ma, non ha gli angoli retti, romboide quella che ha i lati e gli angoli opposti fra loro ma, non è equilatera né, ha gli angoli retti. E le figure quadrilatere oltre a queste si chiamino trapezi

Per approfondimenti
Il paraboloide di Casale Monferrato
http://www.comune.casale-monferrato.al.it/paraboloide

Altri articoli Oicos, della sezione Sito ex Montedison di Assisi
Articolo n° 1 – La fabbrica di perfosfato a Santa Maria di Simone Menichelli